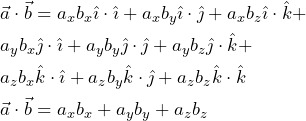Muchas magnitudes físicas conocidas pueden especificarse completamente con un solo número y la unidad apropiada. Por ejemplo, «un periodo de clase dura 50 min» o «el tanque de gasolina de mi auto tiene capacidad de 65 L» o «la distancia entre dos postes es de 100 m». La cantidad física que puede especificarse completamente de esta manera se denomina magnitud escalar. El tiempo, la masa, la distancia, la longitud, el volumen, la temperatura y la energía son ejemplos de magnitudes escalares.
Las cantidades escalares que tienen las mismas unidades físicas pueden sumarse o restarse según las reglas habituales del álgebra de los números. También pueden multiplicarse o dividirse entre sí para formar una cantidad escalar derivada.
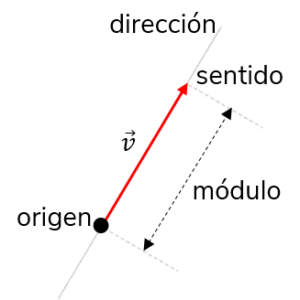
Sin embargo, muchas magnitudes físicas no pueden describirse completamente con un solo número de unidades físicas. Un equipo de rescate debe conocer, no solo la distancia a la que se encuentra la señal de socorro, sino también la dirección de la que procede esta para poder llegar a su origen lo antes posible. Las magnitudes físicas que se especifican completamente con un número de unidades (magnitud) y una dirección se llaman magnitudes vectoriales. Algunos ejemplos de cantidades vectoriales son el desplazamiento, la velocidad, la posición, la fuerza y el momento.
3.1. Definición de vector
En el lenguaje matemático, las cantidades físicas vectoriales se representan mediante objetos matemáticos, denominados vectores. Podemos sumar o restar dos vectores, y podemos multiplicar un vector por un escalar o por otro vector, pero no podemos dividir por un vector. La operación de división por un vector no está definida.
Para distinguir entre una cantidad vectorial y una escalar, adoptamos la convención común de que una letra con una flecha encima denota un vector, ![]() , y una letra sin flecha denota un escalar.
, y una letra sin flecha denota un escalar.
Los vectores se clasifican según diferentes criterios, principalmente su punto de aplicación, relación con otros vectores y características propias.
Clasificación según el punto de aplicación:
- Vectores libres: No tienen un punto de aplicación específico, su efecto es el mismo independientemente de dónde se ubiquen a lo largo de su línea de acción.
- Vectores deslizantes: Pueden deslizarse a lo largo de su línea de acción sin cambiar su efecto.
- Vectores fijos o ligados: Tienen un punto de aplicación definido y su efecto depende de este punto.
Clasificación según la relación con otros vectores:
- Vectores concurrentes o angulares: Sus líneas de acción se intersectan en un punto común.
- Vectores colineales: Sus líneas de acción son la misma recta.
- Vectores paralelos: Sus líneas de acción son paralelas.
- Vectores coplanares: Sus líneas de acción están en el mismo plano.
- Vectores opuestos: Tienen la misma magnitud y dirección pero sentidos contrarios.
- Vectores equipolentes: Tienen la misma magnitud, dirección y sentido, aunque su punto de aplicación puede ser diferente.
Clasificación según características propias:
- Vectores unitarios: Tienen una magnitud de 1.
- Vectores nulos: Tienen una magnitud de 0.
- Vectores axiales o pseudovectores: Están asociados a fenómenos de rotación y su dirección indica el eje de rotación.
3.2. Expresión matemática de un vector
En un sistema de coordenadas XY rectangular (cartesiano) en un plano, un punto en un plano se describe por un par de coordenadas (la x, la y). De forma similar, un vector ![]() en un plano se describe mediante un par de sus coordenadas vectoriales. La coordenada x del vector
en un plano se describe mediante un par de sus coordenadas vectoriales. La coordenada x del vector ![]() se llama su componente x y la coordenada y del vector
se llama su componente x y la coordenada y del vector ![]() se llama su componente y. El componente x del vector es un vector denotado por
se llama su componente y. El componente x del vector es un vector denotado por ![]() . El componente y del vector es un vector denotado por
. El componente y del vector es un vector denotado por ![]() En el sistema cartesiano, los componentes vectoriales x y y de un vector son las proyecciones ortogonales de este vector sobre los ejes de la x y la y, respectivamente.
En el sistema cartesiano, los componentes vectoriales x y y de un vector son las proyecciones ortogonales de este vector sobre los ejes de la x y la y, respectivamente.
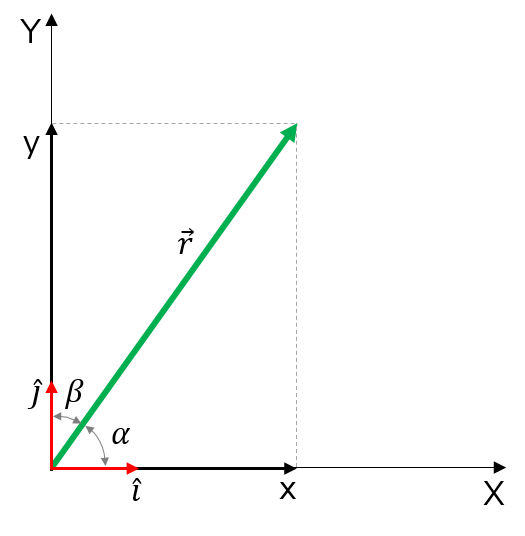
De este modo, siguiendo la regla del paralelogramo para la suma de vectores, cada vector en un plano cartesiano puede expresarse como la suma vectorial de sus componentes vectoriales:
(1) ![]()
Es habitual denotar la dirección positiva en el eje de la x por el vector unitario ![]() y la dirección positiva en el eje de la y por el vector unitario
y la dirección positiva en el eje de la y por el vector unitario ![]() . Los vectores unitarios de los ejes,
. Los vectores unitarios de los ejes, ![]() y
y ![]() , definen dos direcciones ortogonales en el plano. Los componentes x y y de un vector pueden escribirse ahora en términos de los vectores unitarios de los ejes:
, definen dos direcciones ortogonales en el plano. Los componentes x y y de un vector pueden escribirse ahora en términos de los vectores unitarios de los ejes:
(2) 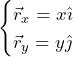
Los vectores ![]() y
y ![]() definidos por la ecuación (2) son los componentes vectoriales del vector
definidos por la ecuación (2) son los componentes vectoriales del vector ![]() . Las cifras
. Las cifras ![]() y
y ![]() que definen los componentes vectoriales en la ecuación (2) son los componentes escalares del vector
que definen los componentes vectoriales en la ecuación (2) son los componentes escalares del vector ![]() . Combinando la ecuación (1) con la ecuación (2), obtenemos la forma en componentes de un vector:
. Combinando la ecuación (1) con la ecuación (2), obtenemos la forma en componentes de un vector:
(3) ![]()
El módulo del vector viene dado por:
(4) ![]()
Los cosenos de los ángulos que forma el vector con los ejes de coordenadas se les denomina cosenos directores, que indican la dirección del vector:
(5) ![]()
Si conocemos las coordenadas A(xa,ya) del punto de origen de un vector y las coordenadas B(xb,yb) del punto final de un vector, podemos obtener los componentes escalares de un vector simplemente al restar las coordenadas del punto de origen de las coordenadas del punto final:
(6) 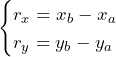
|
Ejemplo A.7 |
Determinación de vectores |
Un puntero de ratón en el monitor de una computadora en su posición inicial está en el punto (6,0 cm, 1,6 cm) con respecto a la esquina inferior izquierda. Si mueve el puntero a un icono situado en el punto (2,0 cm, 4,5 cm), ¿cuál es el vector de desplazamiento del puntero?
SOLUCIÓN
El origen del sistema de coordenadas xy es la esquina inferior izquierda del monitor de la computadora. Por lo tanto, el vector unitario ![]() en el eje de la x apunta horizontalmente a la derecha y el vector unitario
en el eje de la x apunta horizontalmente a la derecha y el vector unitario ![]() en el eje de la y apunta verticalmente hacia arriba. El origen del vector de desplazamiento está situado en el punto A(6,0, 1,6) y el final del vector de desplazamiento está situado en el punto B(2,0, 4,5). Sustituye las coordenadas de estos puntos en la ecuación (4) para encontrar los componentes escalares dx y dy del vector de desplazamiento
en el eje de la y apunta verticalmente hacia arriba. El origen del vector de desplazamiento está situado en el punto A(6,0, 1,6) y el final del vector de desplazamiento está situado en el punto B(2,0, 4,5). Sustituye las coordenadas de estos puntos en la ecuación (4) para encontrar los componentes escalares dx y dy del vector de desplazamiento ![]() . Por último, sustituye las coordenadas en la ecuación (3) para escribir el vector de desplazamiento en forma de componente vectorial.
. Por último, sustituye las coordenadas en la ecuación (3) para escribir el vector de desplazamiento en forma de componente vectorial.
Identificamos xa = 6,0, xb = 2,0, ya = 1,6 e yb = 4,5, donde la unidad física es 1 cm. Los componentes escalares x y y del vector de desplazamiento son
![]()
La forma de componente vectorial del vector de desplazamiento es:
![]()
Cuando conocemos las componentes escalares rx y ry de un vector ![]() , podemos encontrar su módulo r y su ángulo direccional α. El ángulo direccional, o dirección para abreviar, es el ángulo que forma el vector con la dirección positiva en el eje de la x. El ángulo α se mide en la dirección contraria a las agujas del reloj desde el eje de la x+ hasta el vector. Como las longitudes r, rx y ry forman un triángulo rectángulo, están relacionadas por el teorema de Pitágoras:
, podemos encontrar su módulo r y su ángulo direccional α. El ángulo direccional, o dirección para abreviar, es el ángulo que forma el vector con la dirección positiva en el eje de la x. El ángulo α se mide en la dirección contraria a las agujas del reloj desde el eje de la x+ hasta el vector. Como las longitudes r, rx y ry forman un triángulo rectángulo, están relacionadas por el teorema de Pitágoras:
(7) ![]()
El ángulo direccional α de un vector se define a través de la función tangente del ángulo α en el triángulo mostrado en la figura:
(8) ![]()
El cociente del lado adyacente rx a la hipotenusa r es la función coseno (cos) del ángulo direccional α, rx/r = cosα, y el cociente del lado opuesto ry a la hipotenusa r es la función seno (sen) de α, ry/r = senα. Cuando la magnitud r y la dirección α son conocidas, podemos resolver estas relaciones para los componentes escalares:
(9) 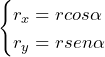
|
Ejemplo A.8 |
Descomposición de vectores |
Un grupo de rescate de un niño desaparecido sigue a un perro de búsqueda llamado Trooper. Trooper deambula y olfatea bastante por muchos senderos diferentes. Finalmente, Trooper encuentra al niño y la historia tiene un final feliz, pero su desplazamiento en diversos tramos luce realmente complejo. En uno de los tramos camina 200,0 m hacia el sureste y luego corre hacia el norte unos 300,0 m. En el tercer tramo, examina cuidadosamente los olores durante 50,0 m en la dirección 30° al oeste del norte. En el cuarto tramo, Trooper va directamente al sur durante 80,0 m. Halle los componentes escalares de los vectores de desplazamiento de Trooper y sus vectores de desplazamiento en forma de componente vectorial para cada tramo.
SOLUCIÓN
Adoptemos un sistema de coordenadas rectangular con el eje de la x positiva en la dirección del este geográfico, con la dirección de la y positiva apuntando al norte geográfico. Explícitamente, el vector unitario ![]() del eje de la x apunta al este y el vector unitario
del eje de la x apunta al este y el vector unitario ![]() del eje de la y apunta al norte. Trooper recorre cinco tramos, por lo que hay cinco vectores de desplazamiento. Comenzamos por identificar sus magnitudes y ángulos direccionales, luego utilizamos la ecuación (7) para encontrar los componentes escalares de cada desplazamiento y la ecuación (3) para los vectores de desplazamiento.
del eje de la y apunta al norte. Trooper recorre cinco tramos, por lo que hay cinco vectores de desplazamiento. Comenzamos por identificar sus magnitudes y ángulos direccionales, luego utilizamos la ecuación (7) para encontrar los componentes escalares de cada desplazamiento y la ecuación (3) para los vectores de desplazamiento.
En el primer tramo, la magnitud del desplazamiento es d1=200,0 m y la dirección es sureste. Para el ángulo direccional α1 podemos tomar cualquiera de los dos 45° medido en el sentido de las agujas del reloj desde la dirección este o 45° + 270° medido en sentido contrario a las agujas del reloj desde la dirección este. Con la primera opción, α1 = −45°. Con la segunda opción, α1 = +315°. Podemos utilizar cualquiera de estos dos ángulos. Los componentes son:
![]()
El vector de desplazamiento del primer tramo es:
![]()
En el segundo tramo de las andanzas de Trooper, la magnitud del desplazamiento es d2 = 300,0 m y la dirección es norte. El ángulo direccional es α2 = +90°. Obtenemos los siguientes resultados:
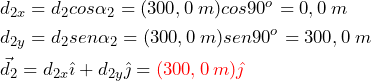
En el tercer tramo, la magnitud del desplazamiento es d3 = 50,0 m y la dirección es 30° al oeste del norte. El ángulo direccional medido en sentido contrario a las agujas del reloj desde la dirección este es α3 = 30° + 90° = +120°. Esto da las siguientes respuestas:
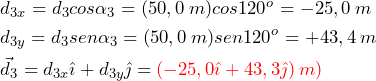
En el cuarto tramo de la excursión, la magnitud del desplazamiento es d4 = 80,0 m y la dirección es sur. El ángulo de dirección puede tomarse como α4 = −90° o α4 = +270°. Obtenemos:
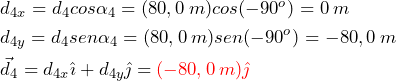
Vectores en tres dimensiones
Para especificar la ubicación de un punto en el espacio, necesitamos tres coordenadas (x, y, z), donde las coordenadas de la x y de la y especifican ubicaciones en un plano, y la coordenada de la z da una posición vertical por encima o por debajo del plano. El espacio tridimensional tiene tres direcciones ortogonales, por lo que no necesitamos dos, sino tres vectores unitarios para definir un sistema de coordenadas tridimensional. En el sistema de coordenadas cartesianas, los dos primeros vectores unitarios son el vector unitario del eje de la x ![]() y el vector unitario del eje de la y
y el vector unitario del eje de la y ![]() . El tercer vector unitario
. El tercer vector unitario ![]() es la dirección del eje z.
es la dirección del eje z.
El orden en que se marcan los ejes, que es el orden en que aparecen los tres vectores unitarios, es importante porque define la orientación del sistema de coordenadas. El orden x-y-z, que equivale al orden ![]() –
– ![]() –
– ![]() , define el sistema de coordenadas estándar de la mano derecha (orientación positiva).
, define el sistema de coordenadas estándar de la mano derecha (orientación positiva).
En el espacio tridimensional, el vector ![]() tiene tres componentes vectoriales: el componente x
tiene tres componentes vectoriales: el componente x ![]() , que es la parte del vector
, que es la parte del vector ![]() a lo largo del eje de la x, el componente y
a lo largo del eje de la x, el componente y ![]() , que es la parte de
, que es la parte de ![]() a lo largo del eje de la y, y el componente z
a lo largo del eje de la y, y el componente z ![]() , que es la parte del vector a lo largo del eje z. Un vector en un espacio tridimensional es la suma vectorial de sus tres componentes vectoriales:
, que es la parte del vector a lo largo del eje z. Un vector en un espacio tridimensional es la suma vectorial de sus tres componentes vectoriales:
(10) ![]()
La magnitud r se obtiene al generalizar la ecuación (4) a tres dimensiones:
(11) ![]()
Los cosenos de los ángulos que forma el vector con los ejes de coordenadas se les denomina cosenos directores, que indican la dirección del vector:
(12) ![]()
3.3. Suma y diferencia de vectores. Producto por un escalar
Suma de vectores
La operación de suma de dos o más vectores da como resultado otro vector. Para realizar la suma de vectores existen distintos métodos, ya sea de manera algebraica o mediante el uso de geometría analítica. El método algebraico es conocido como método directo.
Los métodos usando geometría analítica son conocidos como, el método del polígono que es utilizado para sumar más de dos vectores, el método del triángulo es el caso particular del método del polígono cuando únicamente se suman dos vectores, y el método del paralelogramo igualmente para sumar dos vectores.
Método algebráico
Para sumar dos o más vectores se suman sus respectivas componentes de cada vector. En el caso de dos vectores, la suma se realiza de la siguiente forma:
(13) ![]()
Ejemplo:
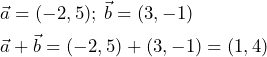
Métodos con geometría analítica
1. Método del triángulo
Para sumar dos vectores libres ![]() y
y ![]() se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
2. Método del paralelogramo
Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.
3. Método del polígono
El método del polígono es utilizado cuando queremos sumar más de dos vectores, y consiste en colocar un vector a continuación del otro, de modo que el extremo de uno coincida con el origen del otro, y así sucesivamente, hasta colocar todos los vectores, la resultante será el vector que cierra el polígono, es decir, es aquel que va desde el inicio del primero al extremo del último vector.


Fig.1.4. Suma de vectores
Diferencia de vectores
La operación de resta de dos o más vectores da como resultado otro vector. Para realizar la resta de vectores existen distintos métodos, ya sea de manera algebraica o mediante el uso de geometría analítica. El método algebraico es conocido como método directo.
Los métodos usando geometría analítica son conocidos como, el método del polígono que es utilizado para restar más de dos vectores, el método del triángulo es el caso particular del método del polígono cuando únicamente se restan dos vectores, y el método del paralelogramo igualmente para restar dos vectores.
Método algebráico
Para restar dos vectores libres ![]() y
y ![]() se suma
se suma ![]() con el opuesto de
con el opuesto de ![]() .
.
Las componentes del vector resta se obtienen restando las componentes de los vectores.
(14) ![]()
Ejemplo:
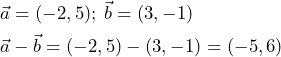
Método de geometría analítica
1. Método del triángulo
Para restar dos vectores libres ![]() y
y ![]() se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
se escogen como representantes dos vectores tales que el extremo de uno coincida con el origen del otro vector.
2. Método del paralelogramo
Se toman como representantes dos vectores con el origen en común, se trazan rectas paralelas a los vectores obteniéndose un paralelogramo cuya diagonal coincide con la suma de los vectores.
3. Método del polígono
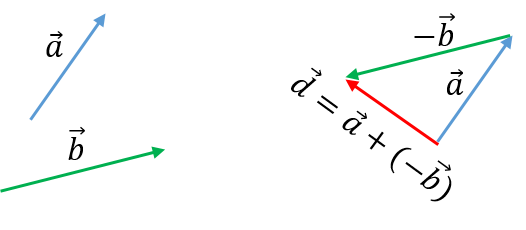
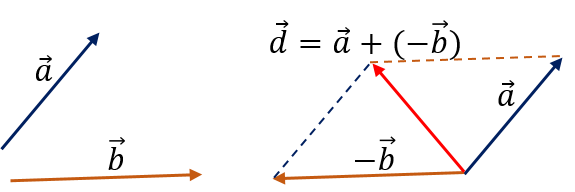
Fig.1.5. Diferencia de vectores
El método del polígono es utilizado cuando queremos restar más de dos vectores, y consiste en colocar un vector a continuación del otro, de modo que el extremo de uno coincida con el origen del otro, y así sucesivamente, hasta colocar todos los vectores, la resultante será el vector que cierra el polígono, es decir, es aquel que va desde el inicio del primero al extremo del último vector.
Producto de un vector por un escalar
Al multiplicar un número por un vector obtenemos otro vector de igual dirección, el sentido será el mismo si el número es positivo, y opuesto en caso de que sea negativo. El módulo será el que resulte de multiplicar el del vector por el número.
Método analítico
Al multiplicar un número real, k, por un vector
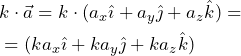
El módulo del nuevo vector vendrá dado por:
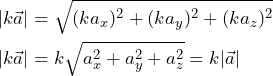
Método gráfico
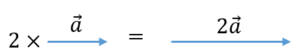

Fig.1.6. Producto de un vector por un escalar
|
Ejemplo A.9 |
Operaciones con vectores |
Sean los vectores ![]() ;
; ![]() . Calcular: a) El módulo de cada uno de ellos; b) El ángulo que forma
. Calcular: a) El módulo de cada uno de ellos; b) El ángulo que forma ![]() con el eje X; c)
con el eje X; c) ![]() ; d)
; d) ![]() ; e) Un vector unitario en la dirección de
; e) Un vector unitario en la dirección de ![]() ; f) Un vector opuesto a
; f) Un vector opuesto a ![]() y módulo 2.
y módulo 2.
SOLUCIÓN
a) Los módulos de los dos vectores vienen dados por:
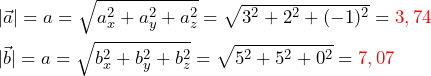
b) Para determinar el ángulo que forma el vector ![]() con el eje X:
con el eje X:
![]()
c) La suma de los dos vectores viene dada por:
![]()
d) Para resolver este apartado solo tenemos que multiplicar el vector ![]() por −2 y sumar el vector
por −2 y sumar el vector ![]() :
:
![]()
e) El vector unitario se obtiene dividiendo el vector entre su módulo:
![]()
f) Se halla el vector unitario en la dirección de ![]() y luego lo multiplicamos por −2:
y luego lo multiplicamos por −2:
![]()
ctividades
- A partir de los vectores
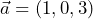 ,
, 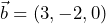 y
y 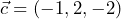 , efectúa las operaciones que se indican: a)
, efectúa las operaciones que se indican: a) 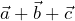 ; b)
; b) 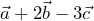 ; c)
; c) 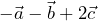 .
.
- Solución: a)
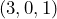 ; b)
; b) 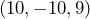 ; c)
; c) 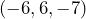 .
.
- Solución: a)
- Dadas tres fuerzas concurrentes, cuyos valores son:
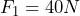 ;
; 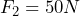 y
y 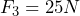 , que forman 30º, 120º y -180º respectivamente con el eje X, calcula: a) La fuerza resultante de sumar las tres; b) El módulo de la resultante y el ángulo que forma con el eje X.
, que forman 30º, 120º y -180º respectivamente con el eje X, calcula: a) La fuerza resultante de sumar las tres; b) El módulo de la resultante y el ángulo que forma con el eje X.
- Solución: a)
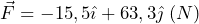 ; b)
; b) 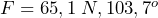
- Solución: a)
3.4. Producto escalar de dos vectores
El resultado de multiplicar escalarmente dos vectores es el número que se obtiene multiplicando sus módulos por el coseno del ángulo que forman:
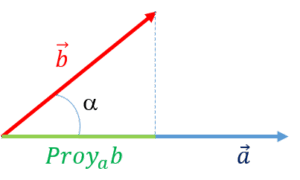
Fig. 1.7 Producto escalar
(15) ![]()
La propia definición nos sirve para determinar el ángulo que forman dos vectores conocidos:
(16) ![]()
Propiedades
- Sí
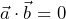 , entonces
, entonces 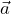 y
y 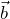 son perpendiculares.
son perpendiculares. 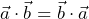 (el producto escalar es conmutativo).
(el producto escalar es conmutativo).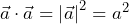 .
.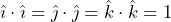 .
.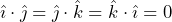 .
.
Procedimiento analítico
Sean los vectores:
(17) 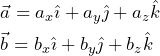
El producto escalar de los dos vectores es:
(18) ![]()
Aplicando la propiedad distributiva:
(19)