El Sistema Internacional de Unidades (SI) es crucial para la ciencia, la tecnología, el comercio y la vida cotidiana, ya que proporciona un sistema coherente y universal de medición. Su importancia radica en garantizar la uniformidad y la precisión en las mediciones, facilitando la comunicación, la colaboración y el avance en diversos campos.
Por otra parte, en física, se utilizan diversas herramientas matemáticas para describir y modelar fenómenos naturales. Estas herramientas van desde conceptos básicos como álgebra y cálculo hasta métodos más avanzados como ecuaciones diferenciales, cálculo vectorial, y teoría de grupos.
En este tema, se trata de revisar los conceptos anteriormente expresados con el fin de abordar en las mejores condiciones la asignatura.
El actual sistema SI es el sistema adoptado internacionalmente, utilizado en la práctica científica y el único legal en España, en la Unión Europea y en numerosos otros países. El SI parte de un pequeño número de magnitudes/unidades denominadas básicas definiendo, a partir de ellas, las denominadas derivadas, como producto de potencias de las básicas. Cuando este producto de potencias no incluye ningún factor numérico distinto de la unidad, estas unidades derivadas se denominan coherentes. Así pues, el SI es un sistema coherente de unidades, que permite cuantificar cualquier magnitud medible de interés en la investigación, la industria, el comercio o la sociedad, en campos tan variados como la salud, la seguridad, la protección del medio ambiente, la adquisición de bienes o la facturación de consumos, por ejemplo.
En 1960, la 11ª Conferencia General de Pesas y Medidas (CGPM) definió y estableció formalmente el SI en su Resolución 12, basado en el anterior sistema métrico decimal. Desde entonces se ha revisado de cuando en cuando, de forma parcial, en respuesta a las necesidades de la ciencia y la tecnología. Ahora, en la segunda década del siglo XXI, se ha revisado en profundidad, basándolo en constantes universales, redefiniéndose sus unidades básicas y variando algunas de sus realizaciones prácticas.
El SI se presenta y define en las publicaciones “SI Brochure”, “Concise Summary” y “Pocket Version”, todas ellas editadas por el BIPM (https://www.bipm.org/en/publications/) y traducidas al español, bajo autorización, por el CEM.
El SI actual consta de siete unidades básicas, más un amplio grupo de unidades derivadas, junto a un conjunto de prefijos adoptados para denominar los valores de aquellas magnitudes que son mucho más grandes o mucho más pequeñas que la unidad básica, y que van desde el prefijo yocto (10-24) hasta el prefijo yotta (1024).
Las siete unidades básicas del SI, establecidas por convenio, se consideran dimensionalmente independientes entre sí y son: metro, kilogramo, segundo, amperio, kelvin, mol y candela.
Las unidades derivadas se forman a partir de las unidades básicas, como productos de potencias de estas. Algunas unidades derivadas reciben nombres especiales, con objeto de expresar, en forma compacta, combinaciones frecuentemente utilizadas de unidades básicas. Así ocurre, por ejemplo, con el julio, símbolo J, por definición igual a kg m2 s-2.
1.1. Magnitudes y unidades fundamentales
El Sistema Internacional de Unidades consta de siete unidades básicas, que expresan magnitudes físicas. A partir de estas se determinan el resto de unidades (derivadas). La última revisión del SI fue aprobada por unanimidad en la 26.ª CGPM, el 16 de noviembre de 2018, acordándose su entrada en vigor el 20 de mayo de 2019, con objeto de hacerlo coincidir con el Día Mundial de la Metrología en el que se conmemora la firma del Tratado de la Convención del Metro en 1875, el más antiguo que existe en vigor.
El SI revisado quedó definido como aquel en el que::
- La frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio-133 (ΔνCs) es 9 192 631 770 Hz.
- La velocidad de la luz en el vacío (c) es 299 792 458 m s-1.
- La constante de Planck (h) es 6.626 070 15 × 10-34 J s.
- La carga elemental (e) es 1.602 176 634 × 10-19 C.
- La constante de Boltzmann (k) es 1.380 649 × 10-23 J K-1.
- La constante de Avogadro (NA) es 6.022 140 76 × 1023 mol-1.
- La eficacia luminosa de la radiación monocromática de 540 × 1012 Hz (Kcd) es 683 lm W-1.
A partir de los valores anteriores se definen las siete unidades básicas:
|
Magnitud |
Nombre |
Símbolo |
Definición |
|
longitud |
metro |
m |
El metro, símbolo m, es la unidad SI de longitud. Se define al fijar el valor numérico de la velocidad de la luz en el vacío, c, en 299 792 458, cuando se expresa en la unidad m s-1, donde el segundo se define en función de la frecuencia del Cesio ΔνCs. |
|
masa |
kilogramo |
kg |
El kilogramo, símbolo kg, es la unidad SI de masa. Se define al fijar el valor numérico de la constante de Planck, h, en 6,626 070 15 x 10−34 , cuando se expresa en la unidad J s, igual a kg m2 s–1, donde el metro y el segundo se definen en función de c y ΔνCs. |
|
tiempo |
segundo |
s |
El segundo, símbolo s, es la unidad SI de tiempo. Se define al fijar el valor numérico de la frecuencia de la transición hiperfina del estado fundamental no perturbado del átomo de cesio 133, ΔνCs, en 9 192 631 770, cuando se expresa en la unidad Hz, igual a s-1. |
|
intensidad de corriente eléctrica |
amperio |
A |
El amperio, símbolo A, es la unidad SI de corriente eléctrica. Se define al fijar el valor numérico de la carga elemental, e, en 1,602 176 634 x 10−19 , cuando se expresa en la unidad C, igual a A s, donde el segundo se define en función de ΔνCs. |
|
temperatura |
kelvin |
K |
El kelvin, símbolo K, es la unidad SI de temperatura termodinámica. Se define al fijar el valor numérico de la constante de Boltzmann, k, en 1,380 649 x 10−23, cuando se expresa en la unidad J K-1, igual a kg m2 s2 K-1, donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs. |
|
intensidad luminosa |
candela |
cd |
La candela, símbolo cd, es la unidad SI de intensidad luminosa en una dirección dada. Se define al fijar el valor numérico de la eficacia luminosa de la radiación monocromática de frecuencia 540 x 1012 Hz, Kcd, en 683, cuando se expresa en la unidad lm W−1, igual a cd sr W−1, o a cd sr kg−1 m−2 s3, donde el kilogramo, el metro y el segundo se definen en función de h, c y ΔνCs. |
|
cantidad de sustancia |
mol |
mol |
El mol, símbolo mol, es la unidad SI de cantidad de sustancia. Un mol contiene exactamente 6,022 140 76 x 1023 entidades elementales. Esta cifra es el valor numérico fijo de la constante de Avogadro, NA, cuando se expresa en la unidad mol-1, y se denomina número de Avogadro. |
Además de las unidades básicas hay dos unidades suplementarias:
|
Magnitud |
Unidad |
Símbolo |
Definición |
|
ángulo plano |
radián |
rad |
Es el ángulo plano comprendido entre dos radios de un círculo que, sobre la circunferencia de dicho círculo, interceptan un arco de longitud igual a la del radio. |
|
ángulo sólido |
estereoradián |
sr |
Es el ángulo sólido que, teniendo su vértice en el centro de una esfera, intercepta sobre la superficie de dicha esfera un área igual a la de un cuadrado que tenga por lado el radio de la esfera. |
1.2. Magnitudes y unidades derivadas
Mediante esta denominación se hace referencia a las unidades utilizadas para expresar magnitudes físicas que tienen una definición matemática en término de magnitudes físicas básicas. Si estas son longitud, masa, tiempo, intensidad de corriente eléctrica, temperatura, cantidad de substancia o intensidad luminosa, se trata de una magnitud básica. Todas las demás son derivadas. No se debe confundir el concepto de unidades derivadas con los de múltiplos y submúltiplos que se utilizan tanto en las unidades básicas como en las derivadas.
Las unidades derivadas coherentes son exactamente aquellas que se pueden obtener mediante una fórmula matemática que las relacione con las unidades básicas que sea de la forma:
![]()
donde a, b, c, d, f, g, h, son números reales puros.
Para cualquier cantidad física, su unidad coherente correspondiente en el SI no es arbitraria sino que se deduce de la fórmula que la relaciona con otra magnitud física previamente definida.
Ejemplos:
- Unidad de volumen: metro cúbico (m³).
- Unidad de densidad: kilogramo por metro cúbico (kg/m³).
- Unidad de aceleración: La aceleración se define por a = d²x/dt². De la definición de la derivada se deduce que si x es un vector con unidad metro y t es un escalar con unidad segundo, entonces a es un vector con unidad metro dividido por el cuadrado del segundo, es decir, metro por segundo cuadrado. Simbólicamente se representa m/s².
- Unidad de fuerza: Está relacionada con la longitud y masa por la segunda ley de Newton: F = m.a. La longitud es una magnitud básica con unidad metro; la aceleración se acaba de tratar en el ejemplo anterior. Usando el álgebra elemental se deduce que la unidad coherente de la fuerza es kg·m/s². Esta unidad tiene el nombre especial de newton (símbolo N).
- Unidad de energía: Se puede expresar en términos de fuerza y distancia por: E = f·l. Se deduce que la unidad coherente es el producto del newton y el metro, es decir, newton·metro (N·m); tiene el nombre especial julio (símbolo J).
Unidades derivadas con nombres especiales
22 unidades derivadas tienen nombres especiales. Para representarlas se pueden usar estos nombres o una expresión algebraica en términos de otras unidades. En algunos casos existe la posibilidad de confusión si se usa u omite un nombre especial aunque esto sea matemáticamente correcto.
|
Magnitud |
Nombre |
Símbolo |
En otras unidades |
En unidades básicas |
Referencia |
|
frecuencia |
hercio |
Hz |
– |
s-1 |
Heinrich Rudolf Hertz |
|
fuerza |
newton |
N |
– |
m kg s-2 |
Isaac Newton |
|
presión |
pascal |
Pa |
N/m2 |
m-1 kg s-2 |
Blaise Pascal |
|
energía |
julio |
J |
N m |
m2 kg s-2 |
James Prescott Joule |
|
potencia y flujo radiante |
vatio |
W |
J/s |
m2 kg s-3 |
James Watt |
|
carga eléctrica |
culombio |
C |
– |
s A |
Charles-Augustin de Coulomb |
|
diferencia de potencial |
voltio |
V |
W/A |
m2 kg s-3 A-1 |
Alessandro Volta |
|
capacidad |
faradio |
F |
C/V |
m2 kg-1 s4 A2 |
Michael Faraday |
|
resistencia eléctrica |
ohmio |
Ω |
V/A |
m2 kg s-3 A-2 |
Georg Simon Ohm |
|
conductancia eléctrica |
siemens |
S |
A/V |
m-2 kg-1 s3 A2 |
Werner von Siemens |
|
flujo magnético |
weber |
Wb |
V s |
m2 kg s-2 A-1 |
Wilhelm Eduard Weber |
|
campo magnético |
tesla |
T |
Wb/m2 |
kg s-2 A-1 |
Nikola Tesla |
|
inductancia |
henrio |
H |
Wb/A |
m2 kg s-2 A-2 |
Joseph Henry |
|
temperatura celsius |
grado celsius |
ºC |
– |
K |
Anders Celsius |
|
actividad catalítica |
katal |
kat |
– |
s-1 mol |
– |
|
actividad radiactiva |
becquerel |
Bq |
– |
s-1 |
Henri Becquerel |
|
dosis absorbida |
gray |
Gy |
J/kg |
m2 s-2 |
Louis Harold Gray |
|
dosis equivalente |
sievert |
Sv |
J/kg |
m2 s-2 |
Rolf Sievert |
|
flujo luminoso |
lumen |
lm |
cd sr |
cd 4π |
– |
|
iluminancia |
lux |
lx |
lm/m2 |
m-2 cd 4π |
– |
|
ángulo plano |
radián |
rad |
– |
m/m |
– |
|
ángulo sólido |
estereorradián |
sr |
– |
m2/m2 |
– |
1.3. Múltiplos y submúltiplos
Para su uso con las unidades SI se proporcionan múltiplos y submúltiplos decimales que van desde 1024 a 10−24. Los nombres y símbolos de los prefijos de estos múltiplos y submúltiplos se presentan en las tabla siguientes.
Los símbolos de los prefijos se escriben con tipo de letra recta, igual que los símbolos de las unidades, independientemente del tipo de letra utilizado en el texto circundante y se unen a los símbolos de las unidades, sin espacio alguno entre el símbolo del prefijo y el símbolo de la unidad. Con la excepción de da (deca), h (hecto) y k (kilo), todos los símbolos de los prefijos de los múltiplos son letras mayúsculas y todos los símbolos de los prefijos de los submúltiplos son letras minúsculas. Todos los nombres de los prefijos se escriben en letras minúsculas, excepto al principio de una frase.
|
Factor |
Nombre |
Símbolo |
|
101 |
deca |
da |
|
102 |
hecto |
h |
|
103 |
kilo |
k |
|
106 |
mega |
M |
|
109 |
giga |
G |
|
1012 |
tera |
T |
|
1015 |
peta |
P |
|
1018 |
exa |
E |
|
1021 |
zetta |
Z |
|
1024 |
yotta |
Y |
|
Factor |
Nombre |
Símbolo |
|
10-1 |
deci |
d |
|
10-2 |
centi |
c |
|
10-3 |
mili |
m |
|
10-6 |
micro |
μ |
|
10-9 |
nano |
n |
|
10-12 |
pico |
p |
|
10-15 |
femto |
f |
|
10-18 |
atto |
a |
|
10-21 |
zepto |
z |
|
10-24 |
yocto |
y |
|
Ejemplo A.1 |
Uso de prefijos |
Replantea la masa 1,93×1013 kg mediante el empleo de un prefijo métrico tal que el valor numérico resultante sea mayor que uno, pero menor que 1000.
SOLUCIÓN
Dado que no se nos permite «duplicar» los prefijos, primero tenemos que replantear la masa en gramos al sustituir el símbolo del prefijo k por un factor de 103. A continuación, debemos ver cuáles de los prefijos se acercan más a la potencia resultante de 10 cuando el número se escribe en notación científica. Utilizamos cualquiera de estos dos prefijos que nos dé un número entre uno y 1000.
Al sustituir la k del kilogramo por un factor de 103, encontramos que
![]()
1016 está entre «peta» (1015) y «exa» (1018). Si utilizamos el prefijo «peta», encontramos que 1,93×1016 g = 1,93×101Pg, dado que 16 = 1 + 15. Alternativamente, si utilizamos el prefijo «exa» encontramos que 1,93×1016 g = 1,93×10−2 Eg, dado que 16 = −2 + 18. Dado que el problema pide el valor numérico entre uno y 1000, utilizamos el prefijo «peta» y la respuesta es ![]() .
.
|
Ejemplo A.2 |
Conversión de unidades |
La distancia de la universidad a casa es de 10 mi (millas) y normalmente tarda 20 minutos en conducir esta distancia. Calcule la rapidez media en metros por segundo (m/s).
SOLUCIÓN
Primero, calculamos la rapidez media con las unidades dadas, luego podemos obtener la rapidez media en las unidades deseadas, al elegir los factores de conversión correctos y multiplicar por estos. Los factores de conversión correctos son los que anulan las unidades no deseadas y dejan en su lugar las unidades deseadas. En este caso, queremos convertir millas a metros, por lo que necesitamos saber que hay 1 609 m en 1 mi. También queremos convertir minutos a segundos, por lo que utilizamos la conversión de 60 s en 1 min.
1. Calculamos la rapidez media. La rapidez media es la distancia recorrida, dividida entre el tiempo de viaje. En forma de ecuación,
![]()
2. Sustituye los valores dados para la distancia y el tiempo:
![]()
3. Convertimos las millas por minuto en metros por segundo al multiplicar por el factor de conversión que anula las millas y deja los metros, y también por el factor de conversión que anula los minutos y deja los segundos:
![]()
|
Ejemplo A.3 |
Conversión de unidades |
La densidad del hierro es 7,86 g/cm3 en condiciones normales. Convierta esto a kg/m3.
SOLUCIÓN
Necesitamos convertir los gramos en kilogramos y los centímetros cúbicos en metros cúbicos. Los factores de conversión que necesitamos son 1 kg = 103 g y 1 cm = 10−2 m. Sin embargo, estamos tratando con centímetros cúbicos (cm3 = cm×cm×cm), por lo que tenemos que utilizar el segundo factor de conversión tres veces (es decir, tenemos que elevarlo al cubo). La idea sigue siendo multiplicar por los factores de conversión de forma que se anulen las unidades que queremos eliminar y se introduzcan las que queremos mantener.
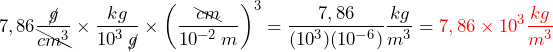
ctividades
- Replantea 4,79 × 105kg utilizando un prefijo métrico tal que el número resultante sea mayor que uno, pero menor que 1000.
- La luz viaja alrededor de 9 petámetros (Pm) en un año. Dado que un año es aproximadamente 3 × 107 s, ¿cuál es la velocidad de la luz en metros por segundo?
- Sabemos que el diámetro de la Tierra es del orden de 107 m, por lo que el orden de magnitud de su área de superficie es de 1014 m2. ¿Cuánto es eso en kilómetros cuadrados (es decir, km2)? (Intenta hacerlo tanto al convertir 107 m a km y luego elevar al cuadrado como al convertir 1014 m2 directamente a kilómetros cuadrados. Debería obtener la misma respuesta en ambos casos).
Centro Español de Metrología
El Sistema Internacional de Unidades